Multiple Choice
Identify the
choice that best completes the statement or answers the question. Write the letter of your choice in
the appropriate space on the Answer Sheet.
|
|
|
1.
|
Which relation is not a function?
|
|
|
2.
|
What is the range of the function? 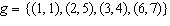 a. | R = {1, 5, 4, 7} | c. | R = {1, 2, 3, 4, 5, 6, 7} | b. | R = {1, 2, 3,
6} | d. | R = {2, 5, 4,
7} |
|
|
|
3.
|
Evaluate 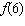 for {(0, 6), (3, 12), (6, 54), (2, 6)}.
|
|
|
4.
|
A car salesman is paid a commission based on the function 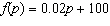 where
p is the sale price of a vehicle. How much will he earn from a car that sells for $15
000?
|
|
|
5.
|
Evaluate 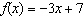 if x = -2
|
|
|
6.
|
Which relation is a function?
|
|
|
7.
|
Which function includes a translation of 3 units to the left?
|
|
|
8.
|
Which equation shows a translation of 3 left and vertical compression by a
factor of 2 to the graph of 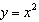 ?
|
|
|
9.
|
Kevin threw a ball straight up with an initial speed of 20 metres per second.
The function 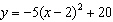 describes the ball’s height, in metres, t
seconds after Kevin threw it. What are the coordinates of the vertex?
|
|
|
10.
|
What are the domain and range of the function 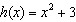 ?
|
|
|
11.
|
Which graph of the given quadratics shows the range R = { y 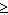 1| y
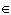 R R}
|
|
|
12.
|
Expand and simplify 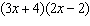 .
|
|
|
13.
|
Which shows the polynomial fully factored? 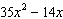
|
|
|
14.
|
Which shows the factorization of the polynomial? 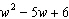
|
|
|
15.
|
Factor the quadratic equation fully. 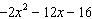
|
|
|
16.
|
Factor the trinomial 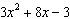 .
|
|
|
17.
|
Which shows the factors of the trinomial? 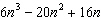
|
|
|
18.
|
Which shows the factorizations of the polynomial 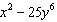 ?
|
|
|
19.
|
Which shows the quadratic function expressed in factored form? 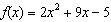
|
|
|
20.
|
What is the axis of symmetry for the function 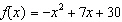 ? a. | x = -3 | c. | x = 6.5 | b. | x =
3.5 | d. | x =
10 |
|
|
|
21.
|
A rocket is shot into the air. The height of the rocket is modelled by the
function 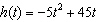 , where h( t) is the height in metres and
t is the time in seconds. When will the rocket hit the ground? a. | 4.5 seconds | c. | 9 seconds | b. | 5 seconds | d. | 45 seconds |
|
|
|
22.
|
What are the coordinated of the vertex of 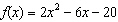 ? a. | (-2, 5) | c. | (-2,
-24) | b. | (1.5, -24.5) | d. | (5, 0) |
|
|
|
23.
|
A fountain shoots water from a nozzle at its top. The function 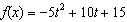 describes
the height of the water h( t), in metres, t seconds after it leaves the nozzle.
What is the maximum height of the water spout? a. | 1 metre | c. | 15 metres | b. | 3 metres | d. | 20 metres |
|
|
|
24.
|
Solve. 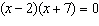 a. | x = -2, 7 | c. | x = 2, -7 | b. | x = 2, 7 | d. | x = -2, -7 |
|
|
|
25.
|
For which quadratic equation is x = 2 a root of the equation?
|
|
|
26.
|
Use factoring to solve 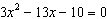 . a. | x = 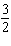 and x = 5 and x = 5 | c. | x = 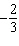 and
x = -5 and
x = -5 | b. | x = 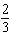 and x = -5 and x = -5 | d. | x = 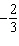 and x = 5 and x = 5 |
|
|
|
27.
|
A skateboard company models its profit with the function P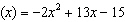 , where x is the number, in thousands, that the company sells, and
P( x) is the profit in tens of thousands of dollars. How many skateboards must the
company sell to break even? Use factoring to solve. a. | at 1500 and 5000 skateboards | c. | at 1.5 and 5
skateboards | b. | at 150 and 500 skateboards | d. | at 1500 and 50 000 skateboards |
|
|
|
28.
|
Which coordinate is the vertex of the function 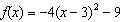 a. | (12, –9) | c. | (3, –9) | b. | (9, –3) | d. | (3, 9) |
|
|
|
29.
|
Which function represents 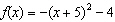 written in standard form?
|
|
|
30.
|
Which equation represents the equation of the axis of symmetry for 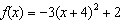 ?
|
|
|
31.
|
Which graph represents the function 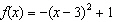 ?
|
|
|
32.
|
What is the factored form of 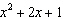
|
|
|
33.
|
What information can you gather immediately from a quadratic function written in
standard form?
a. | vertex | c. | y-intercept | b. | equation of the axis of
symmetry | d. | domain |
|
|
|
34.
|
Identify the values of a, b, and c you would use to
substitute into the quadratic formula to solve 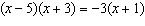 (Remember: your equation needs
to be in standard form 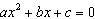 ). a. | a = –5; b = 3; c = –3 | c. | a = 1; b = –5;
c = –18 | b. | a = 1; b = 5; c =
–18 | d. | a = 1;
b = 1; c = –12 |
|
|
|
35.
|
Use the quadratic formula to solve 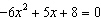 . Round your answer to two decimal
places. a. | –0.81 | c. | –0.81 and 1.64 | b. | 1.64 | d. | no real
solution |
|
|
|
36.
|
Use the quadratic formula to solve 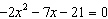 . Round your answer to two decimal
places. a. | –5.43 and 1.93 | c. | –4.5 and 0.98 | b. | –1.93 and 5.43 | d. | no real
solution |
|
|
|
37.
|
A golf ball is chipped out of a sand trap along a path that can be modelled by
the quadratic function 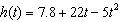 , where time, t, is in seconds and height,
h( t), is in metres. Use the quadratic formula to determine where the ball will land to
the nearest hundredth. a. | 0 m | c. | 7.26 m | b. | 4.81 m | d. | 88.47 m |
|
|
|
38.
|
A disc is thrown into the air and follows a path modelled by the function 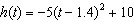 , where time, t, is in seconds and height, h( t), is in metres. When
does the disc hit the ground again? a. | 1.0 s | c. | 2.8 s | b. | 1.4 s | d. | 3.0 s |
|
|
|
39.
|
A rocket is launched into the sky and follows a path modelled by the function
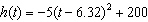 , where time, t, is in seconds and height, h( t), is in metres.
Approximately how high will the rocket be after 9 seconds? a. | 145 m | c. | 187 m | b. | 164 m | d. | 200 m |
|
|
|
|
|
|
40.
|
Given the triangle above, if a = 9, b
= 15, and c = 12, what are the primary trigonometric ratios for
ÐA?
|
|
|
41.
|
Given triangle ABC above, if ÐA
= 38° and b = 4.47 cm, determine a to the nearest hundredth.
a. | 7.26 cm | c. | 3.52 cm | b. | 2.75 cm | d. | 5.67 cm |
|
|
|
42.
|
Given the figure above, if a = 3.4 m and
c = 1.8 m, determine ÐC to the nearest degree.
|
|
|
43.
|
The tallest church tower in the Netherlands is the Dom Tower in Utrecht.
If the angle of elevation to the top of the tower is 77° when 25.9 m
from the base, what is the height of the Dom Tower to the nearest metre.
a. | 25 m | c. | 112 m | b. | 115 m | d. | 27 m |
|
|
|
44.
|
Guillermo is standing 112.5 m from an office building. The top of the
building is at an angle of elevation of 39°. If
Guillermo’s eyes are 1.6 m off the ground, what is the height of the building to the nearest
tenth of a metre?
a. | 87.4 m | c. | 89.0 m | b. | 92.7 m | d. | 91.1 m |
|
|
|
|
|
|
45.
|
Given the figure above, if l = 3.4, ÐJ = 28°,
and j = 3.2, use the sine law to determine ÐL to the nearest degree.
|
|
|
|
|
|
46.
|
Given the figure above, if ÐDCA =
106°, b = 27.6 cm, and c = 41.3 cm, use the sine law to
calculate ÐB to the nearest degree.
a. | 55° | c. | 40° | b. | 44° | d. | none of the above |
|
|
|
|
|
|
47.
|
For triangle HIJ, if ÐI = 70°, j = 5.35 cm, and h = 3.80 cm, use the cosine law to solve
for side i. Round your answer to the nearest hundredth of a centimetre.
a. | 29.16 cm | c. | 5.40 cm | b. | 5.40 cm | d. | none of the
above |
|
|
|
48.
|
For triangle HIJ, if h = 46, i = 73, and j = 58, use
the cosine law to solve for ÐI. Round your answer to the
nearest degree.
|
|
|
49.
|
Using triangle GHI below, if ÐG
and i are known, which can be used to solve for g? 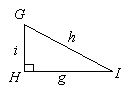 a. | sine law | c. | both a and b | b. | primary trigonometric
ratios | d. | neither a nor
b |
|
|
|
|
|
|
50.
|
Given triangle DEF, if e, d, and f are known, which
can be used to solve for ÐF?
a. | sine law | c. | primary trigonometric ratios | b. | cosine
law | d. | none of the
above |
|
|
|
51.
|
Given triangle DEF, if ÐD, ÐE, f, and e are known, which can be used to solve for
d?
a. | sine law | c. | either a or b | b. | cosine law | d. | neither a nor b |
|
|
|
52.
|
The graph depicts the height in metres of a bouncing ball with respect to time
in seconds (given the friction in the environment to be negligible). What is the period of the
graph? 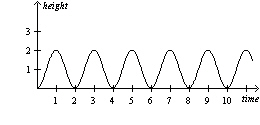 a. | 2 seconds | c. | 4 seconds | b. | 10 seconds | d. | 5 seconds |
|
|
|
53.
|
What is the equation of the axis?
a. | the horizontal line that intersects the maximum value of a periodic
function | b. | twice the sum of the maximum and minimum functional values | c. | the
y-intercept of a periodic function | d. | the horizontal line halfway between the maximum
and minimum value of a periodic function |
|
|
|
54.
|
What is the amplitude?
a. | the distance between the maximum and minimum values of the
function | b. | the length of one cycle | c. | the distance between the equation of the axis
and either a maximum or minimum value of the function | d. | the number of cycles
shown |
|
|
|
55.
|
What is the amplitude of the function? 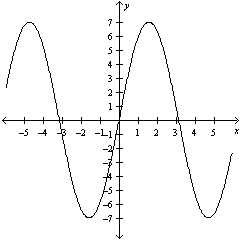
|
|
|
56.
|
Consider a Ferris wheel which loads passengers at a height of 1 metre above the
ground a carries them to a height of at most 15 metres. What is the amplitude of the function which
models the height of a passenger above ground while in constant motion?
|
|
|
57.
|
What can be modelled by a sinusoidal function?
a. | the temperature of a cooler with respect to time | b. | the motion of a kite
with respect to time | c. | the balance of a mortgage with respect to
time | d. | the height of a boy on a swing with respect to time |
|
|
|
58.
|
State the transformation of f(x) = sin x + 4.
a. | horizontal translation left 4 units | b. | vertical translation downward 4
units | c. | vertical translation upward 4 units | d. | horizontal translation right 4
units |
|
|
|
59.
|
State the transformation of f(x) = sin(x – 30°)
a. | horizontal translation right 30° | c. | vertical
translation upward 30° | b. | horizontal translation left 30° | d. | vertical translation downward 30° |
|
|
|
60.
|
What is the equation of the axis of the graph? 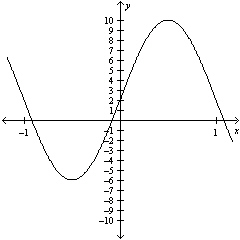 a. | y = 2 | c. | y = 7 | b. | x = 2 | d. | x = 7 |
|
|
|
61.
|
What is the amplitude of the function 3sin(x – 4)?
|
|
|
62.
|
Which of the following is equivalent to 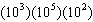 ?
|
|
|
63.
|
Which of the following is equivalent to 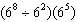 ?
|
|
|
64.
|
Which of the following is equivalent to 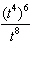 ?
|
|
|
65.
|
Simplify 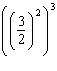 .
|
|
|
66.
|
Which of the following is equivalent to 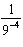 ?
|
|
|
67.
|
Evaluate 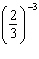 .
|
|
|
68.
|
Which of the following is equivalent to 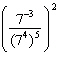 ?
|
|
|
69.
|
Write 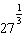 in radical form.
|
|
|
70.
|
Write 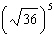 in exponential form.
|
|
|
71.
|
Left untreated, algae in a reservoir reproduce at the rate of 5% per week.
Currently, the algae cover one eighth of the reservoir. An algebraic model of this situation is 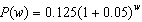 , where 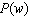 is the percent covered after w weeks. What does
0.125 represent in this situation? a. | the depth of the algae in the water | b. | the fraction of the algae that reproduce each
week | c. | the rate of algae reproduction per week | d. | the initial
percentage of the reservoir that is covered by algae |
|
|
|
72.
|
Left untreated, algae in a lake reproduce at the rate of 4.5% per week.
Currently, the algae cover one tenth of the reservoir. An algebraic model of this situation is 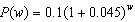 , where 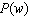 is the percent covered after w weeks. If the
algae continues to go untreated, what percentage of the reservoir will be covered in algae 15 weeks
from now? Round your answer to the nearest percent.
|
|
|
73.
|
There are 2000 yeast cells in a culture. The number of cells grows at a rate of
15% per day. The function that models the growth of the yeast cells is 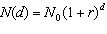 , where N is
the number of yeast cells d days after the culture is started, 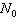 is the initial
population, and r is the growth rate. How many cells will there be in the culture after two
weeks? Round your answer to the nearest whole number. a. | 5 290 000 | c. | 2645 | b. | 21 347 | d. | 14 151 |
|
|
|
74.
|
Identify the growth rate in the following algebraic model: 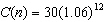 .
|
|
|
75.
|
In the following exponential growth model, what does the 0.35 represent? 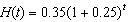 a. | the growth rate | b. | the initial amount | c. | the time since the
initial period | d. | the percent that doubles in t time periods |
|
|
|
76.
|
A new car costs $26 000. It loses 16% of its value each year after it is
purchased. Determine the value of the car after 40 months.
a. | $11 938.38 | c. | $2433.02 | b. | $5781.49 | d. | $14 540.22 |
|
|
|
77.
|
Darien borrows $4265 to help pay for university tuition at an annual rate of 7%.
He starts to pay for the simple interest loan in 4 years. How much interest will have been added to
the loan at that time?
a. | $1194.20 | c. | $5459.20 | b. | $1325.54 | d. | $5590.54 |
|
|
|
78.
|
An investment of $850 earns 6.75%/a. Calculate the value of the investment when
the interest is compounded quarterly for 5 years.
a. | $1187.87 | c. | $3138.89 | b. | $924.18 | d. | $1178.31 |
|
|
|
79.
|
Calculate the amount you would end up with if you invested $4000 at 11.2%
compounded monthly for 5 years.
a. | $6801.17 | c. | $4190.18 | b. | $6984.53 | d. | $4471.73 |
|
|
|
80.
|
Yelena inherits $125 000. She wants to invest part of it for her college fund.
How much should she invest in a GIC earning 9.5%/a compounded monthly to ensure that she has $100 000
in savings 3 years from now?
a. | $33 653.53 | c. | $90 971.32 | b. | $59 687.94 | d. | $75 285.86 |
|
|
|
81.
|
Determine the present value of a loan of $24 150 that is due in 7 years. The
interest rate is 8%/a compounded quarterly.
a. | $14 091.29 | c. | $21 024.03 | b. | $2799.32 | d. | $13 871.15 |
|
|
|
82.
|
Over the course of 8 years, Serge makes deposits of $250 every 6 months into an
account that pays 3.75%/a interest compounded semi-annually. How much interest will Serge have earned
over the 8-year term?
a. | $722.09 | c. | $136.29 | b. | $1369.88 | d. | $614.86 |
|
|
|
83.
|
Calculate the regular deposit made four times a year for 6 years at 7%/a
compounded quarterly that will accumulate to an amount of $8000.
a. | $559.18 | c. | $67.03 | b. | $638.09 | d. | $271.09 |
|
|
|
84.
|
How much should be deposited into an account to set up an annuity that will
provide equal payments of $100 per month over the next 4 years? The annuity will earn 4.8%/a
compounded monthly.
a. | $3876.32 | c. | $1863.84 | b. | $2734.92 | d. | $4359.42 |
|
|
|
85.
|
A $21 000 car loan is charged 3.9%/a interest compounded monthly. Determine the
monthly payments needed to pay the loan off in 5 years.
a. | $385.80 | c. | $291.35 | b. | $350.03 | d. | $300.84 |
|