Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
If 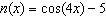 , determine 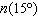 .
|
|
|
2.
|
Determine the period of the function 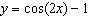 .
|
|
|
3.
|
A spring bounces up and down according to the model 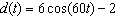 , where 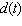 is the
displacement in cm from the rest position and t is time in seconds. What is the
range?
|
|
|
4.
|
Which of the following situations would not produce a periodic graph?
a. | A nail is stuck in the wheel of a car moving at a constant velocity.
•
independent variable: time
• dependent variable: height of nail above
ground | b. | Waves move past a dock post in the ocean during stormy weather.
•
independent variable: time
• dependent variable: height of water on post | c. | A pendulum swings in
a grandfather clock.
• independent variable: time
• dependent variable: horizontal
distance of pendulum from center of clock | d. | A piston moves back and forth in the engine of
a train travelling at a constant velocity.
• independent variable: time
• dependent
variable: horizontal position of piston |
|
|
|
5.
|
Which of the following situations would produce a periodic graph?
a. | passing a basketball, but the ball misses the target and just bounces along the
ground | b. | a machine that cuts a board every 10 s | c. | a biker’s pace through a mountainous
terrain | d. | jumping as high as you can for 10 straight minutes |
|
|
|
6.
|
Frank is riding a Ferris wheel, where t is time in seconds. Suppose
the Ferris wheel is 20 m tall. Let 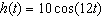 represent the height of Frank in m above
or below the centre of the Ferris wheel. How long does it take to make two complete cycles on
the Ferris wheel? Assume there are no stops. a. | 60 s | c. | 45 s | b. | 30 s | d. | 120 s |
|
|
|
7.
|
The graph of a periodic function is shown below. What is the period of the
function? 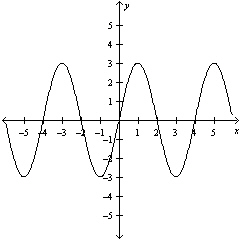
|
|
|
8.
|
Tasha is swinging back and forth on a swing. Her motion is given by the
following graph, where positive numbers refer to her being in front of the starting position and
negative numbers refer to her being behind the starting position. 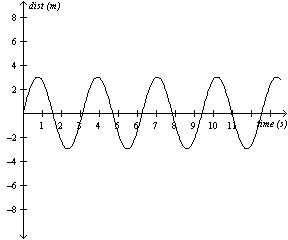 If Tasha starts at the
resting position, how long does it take her to return to that spot?
|
|
|
9.
|
The graph of a periodic function is shown below. What is the amplitude of
the function? 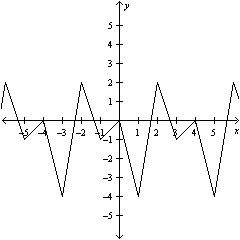
|
|
|
10.
|
Determine the amplitude of the function 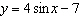 . a. | 7 | c. | 4 | b. | 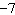 | d. | 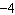 |
|
|
|
11.
|
Suppose the following graph represents a water slide that Kim goes down.
She decides that she will ride the slide 4 times in a row. Assuming Kim goes down the slide at
the same rate each time, which of the following will ensure that the water slide activity will be
periodic? 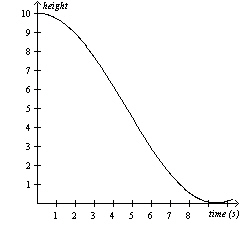 a. | she does not take a 5 minute break after each trip down the slide | b. | she gets out of the
pool as fast as possible each time | c. | she goes to get a drink after one of the
trips | d. | the time in between sliding stays the same |
|
|
|
12.
|
A motorcycle race is taking place on a flat surface 3 m above the ground.
Suppose one of the bike wheels has a radius of 37 cm and it has a nail stuck in it. What is the
maximum height that the nail obtains with respect to the ground?
a. | 37 cm | c. | 74 cm | b. | 337 cm | d. | 374 cm |
|
|
|
13.
|
Without graphing, determine the equation of the axis of the function 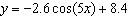 .
|
|
|
14.
|
The displacement of a buoy in metres in the water is described by the function
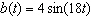 at time t seconds. If the buoy starts at the center, when is the second time
that the buoy will be back at the center?
|
|
|
15.
|
Without graphing, determine the period of the function 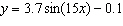 .
|
|
|
16.
|
If 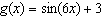 , determine 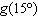 .
|
|
|
17.
|
For the following table of data, determine an equation of a cosine function that
satisfies the given data.
|
|
|
18.
|
A rock is caught in the tire of a bicycle. The height of the rock is
represented by the following graph. 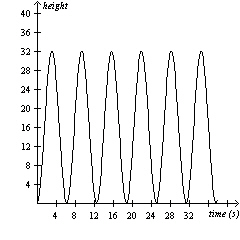 If the rock finally fell out after 6
periods, how long was the rock stuck in the tire?
|
|
|
19.
|
The average number of customers per day that enter the retail store Bathing
Suits Unlimited in terms of the day of the year is modelled by the equation 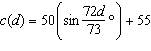 , where
c is the number of customers and d is the day of the year, with 0 representing March 1.
What does the 55 in the equation represent? a. | The difference between the busiest day and the slowest day. | b. | The halfway point
between the busiest day and the slowest day. | c. | The difference between the busiest day and the
halfway point to the slowest day. | d. | The busiest
day. |
|
|
|
20.
|
The height of a saw tooth in inches after time in seconds is represented by the
following graph. Determine the value of k for the function. 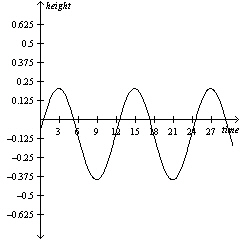
|
|
|
21.
|
The height of a saw tooth in inches after time in seconds is represented by the
function 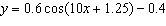 for t > 0. Without graphing the function, determine the minimum height
that the saw tooth reaches.
|
|
|
22.
|
Zontini the Amazing Hypnotist is hypnotizing a volunteer at a performance by
swinging a pocket watch back and forth in front of her face. The pocket watch’s current
distance from center in centimetres in terms of time is modelled by the equation 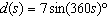 . If Zontini
the Amazing Hypnotist were to swing the watch twice as fast, covering the same distance, how would
the equation change?
|
|
|
23.
|
Which of the following does the function 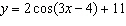 not have? a. | reflection | c. | vertical stretch | b. | horizontal shift | d. | vertical shift |
|
|
|
24.
|
The graph of a periodic function is shown below. What is the equation of
axis of the function? 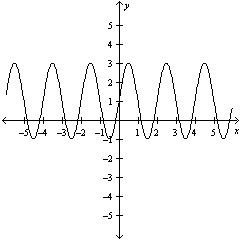
|
|
|
25.
|
Which of the following does not make sense?
a. | period of 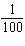 | c. | amplitude of 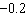 | b. | vertical stretch by a factor of 0.005 | d. | horizontal shift 3 units
left |
|
|
|
26.
|
Alicia is playing the piano. Her metronome ticks every time the pendulum rod
reaches its farthest point from center. The location of the tip of the pendulum rod compared to the
center of the metronome in terms of seconds passed is modelled by the equation 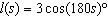 . How many
beats per minute (bpm) is the metronome set to? a. | 180 bpm | c. | 90 bpm | b. | 60 bpm | d. | 120 bpm |
|
|
|
27.
|
The height of a saw tooth in inches after time in seconds is represented by the
function 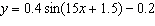 for t > 0. Without graphing the function, determine the maximum height
that the saw tooth reaches. a. | 0.2 in. | c. | 0.4 in. | b. | 0.3 in. | d. | 1.5 in. |
|
|
|
28.
|
Determine the correct equation of the following graph. 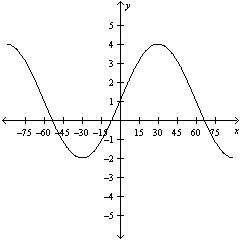
|
|
|
29.
|
For the following table of data, determine an equation of a sine function that
satisfies the given data.
|
|
|
30.
|
Determine the equation of a sine function that would have a range of 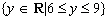
and a period of 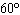 .
|
|
|
31.
|
Which of the following does the function 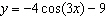 not have? a. | reflection | c. | vertical shift | b. | horizontal shift | d. | horizontal
stretch |
|
|
|
32.
|
A hamster is running in a hamster wheel that is 2 cm off the ground and whose
diameter is 8 cm. The hamster trips from going so fast and the wheel itself begins to spin the
hamster around. The hamster is at the bottom of the wheel when it trips and makes 4 rotations per
second. Which equation roughly models the hamster’s distance from the ground in terms of
time?
|
|
|
33.
|
The temperature each hour in Elma, Texas on October 1 is modelled by the
equation 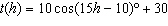 where h is hour of the day with 0 meaning midnight, and t is the
temperature in degrees Celsius. How hot did it get in Elma on October 1?
|
|
|
34.
|
A sinusoidal function has an amplitude of 4.6 units, a period of 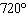 , and a
maximum at (0, 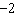 ). Determine an equation of the function.
|
|
|
35.
|
Hans is jumping on a trampoline. His distance from the ground, in metres, in
terms of time, is modelled by the equation 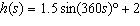 . What does the 2 in this equation
represent? a. | The height of the trampoline | b. | Hans’ lowest distance from the ground in
metres | c. | Hans’ average distance from the ground in metres | d. | The total distance
Hans is covering each jump |
|
|
|
36.
|
As Ricky rides his rocking horse, the distance from the horse’s tail to
the ground, in centimetres, in terms of seconds, is modelled by the equation 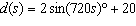 . How long
does it take for the tail to go all the way up and all the way down once?
|
|
|
37.
|
Determine the correct equation of the following graph. 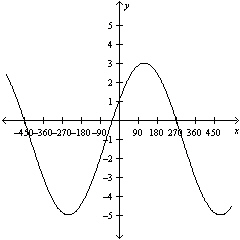
|
|
|
38.
|
A sinusoidal function has an amplitude of 0.75 units, a period of 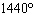 ,
and a maximum at (0, 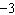 ). Determine an equation of the function.
|
Short Answer
|
|
|
39.
|
A table of values is shown below. Is there enough information to determine
whether the data might represent a periodic function? Justify your answer. x | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | y | 10 | 5 | 2 | 0 | 2 | 5 | 10 | 17 | | | | | | | | | |
|